Introduction
Welcome to my article, we are going to talk about binary operators in Go 😀
With this functionality, we can perform operations with binary numbers. For example, we can have a variable 'A' representing a binary number, another variable 'B', and use logical operators to perform operations that will result in a value 'X'
| A | B | X |
|---|---|---|
| 101 | 100 | ? |
| 001 | 111 | ? |
Logical Operators
We use logical operators to compare two values. They allow us to combine two values and obtain a result of either 1(one) or 0(zero).
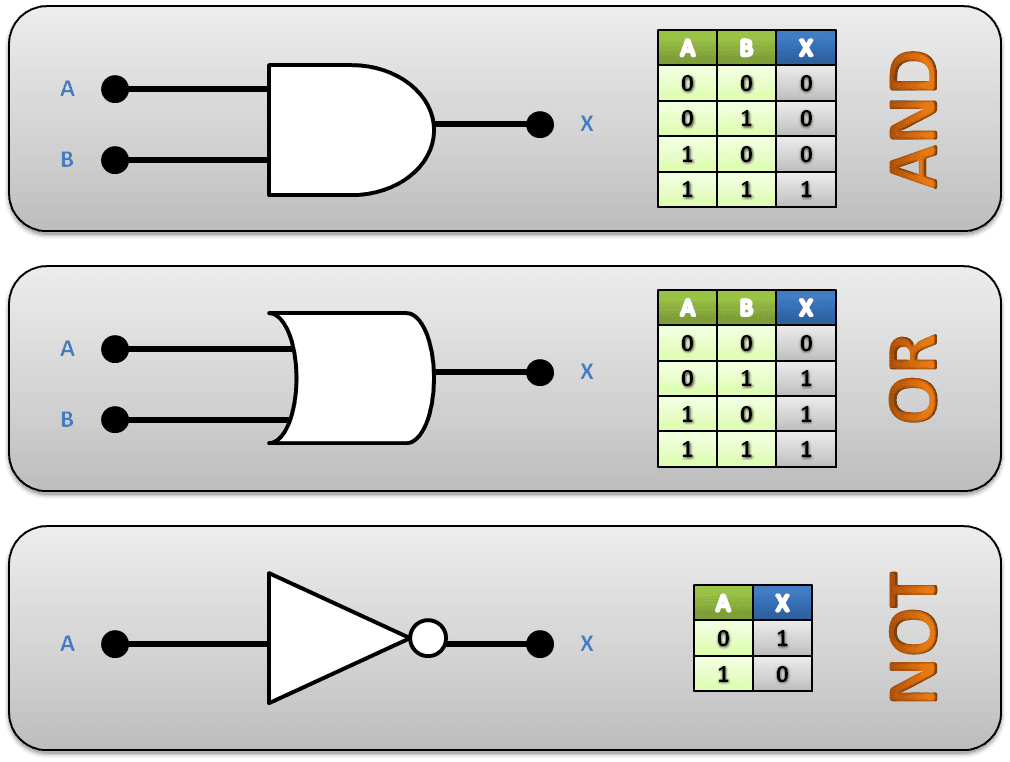
There are 3 common operators: AND, OR and NOT. In our examples, we will use variables A and B as input, and variable X as the output.
AND
When A and B are both 1, X is 1. Otherwise, X is 0.
OR
When A or B is 1, X is 1.
The only case where X can be 0 is when A and B are both 0
NOT
Unlike the other logical operators, NOT only takes one input value, and the value of X will always be the opposite of A
If A is 1, X will be 0, and if A is 0, X will be 1
There are other Logical Operatos that we are going to explain next:
XOR
XOR is equal to OR, however with a difference: if A and B are both 1, X will be 0. X is 1 when A and B aren't both the same value.
For example: if A and B are both 1, X will be 0. if A and B are both 0, X will be 0 too. Otherwise, X will be 1
NAND
NAND is the opposite of AND (AND + NOT). X will be 0 when A and B are both 1. Otherwise, X will be 1
NOR
NOR is the opposite of OR (OR + NOT), if A and B are both 0, X will be 1. Otherwise, X will be 0
XNOR
XNOR is the opposite of XOR (XOR + NOT), X will be 1 when A and B are both the same value

Binary Operators in Go
For the next examples, we are going to use a 16-bit positive integer value (uint). We will set it to a decimal value and display the value in both decimal and binary formats in the console.
(We will use %b to see its binary representation.)
var a uint16 = 213
fmt.Printf("Number %d in binary is %b\n", a, a)Output:
Number 213 in binary is 11010101Left shift & Right shift
We use those operators to shift the binary values by n positions.
Left shift is represented by <<, for example:
// binary_number << n_positions_to_shift = result
fmt.Printf("Number %d in binary is %b\n", a << 1, a << 1)
// 11010101 << 1 = 110101010 (We shift it once)
fmt.Printf("Number %d in binary is %b\n", a << 10, a << 10)
// 11010101 << 10 = 101010000000000 (We shift it 10 times)Output:
Number 426 in binary is 110101010
Number 21504 in binary is 101010000000000The result is 101010000000000 instead of 110101010000000000. When we attempt to perform a left shift with 10 positions, the value is truncated. This happens because the value being shifted is bigger than 16 bits.
Right shift is represented by >>, for example:
// binary_number >> n_positions_to_shift = result
fmt.Printf("Number %d in binary is %b\n", a >> 1, a >> 1)
// 11010101 >> 1 = 1101010 (We shift it once, the number will be decreasing)
fmt.Printf("Number %d in binary is %b\n", a >> 10, a >> 10)
// 11010101 >> 10 = 0 (We shift 10 times)
fmt.Printf("Number %d in binary is %b\n", a >> 5, a >> 5)
// 11010101 >> 10 = 110 (We shift 5 times)Output:
Number 106 in binary is 1101010
Number 0 in binary is 0
Number 6 in binary is 110There will come a point where we won't be able to decrement it anymore, and it will always be zero. For example, when we tried to shift it 10 times.
Logical Operators
We are going to declare another variable to perform the following examples.
(We will use a 10-digit format to fill it with leading zeros)
var b uint16 = 20
fmt.Printf("'a': %.3d - %.10b\n", a, a) // a = 0011010101
fmt.Printf("'b': %.3d - %.10b\n\n", b, b) // b = 0000010100Output:
'a': 213 - 0011010101
'b': 020 - 0000010100Representation of the binary logical operators in Go:
- If we want to perform an AND operation between A and B, we use: a & b
- If we want to perform an OR operation between A and B, we use: a | b
- If we want to perform an XOR operation between A and B, we use: a ^ b
- If we want to perform a NOT operation on A, we use: ^a
(The caret symbol (^) is indeed used for both XOR and NOT operations.)
// AND
fmt.Printf("Bitwise AND: %d - %.10b\n", a & b, a & b)
// 0011010101 AND 0000010100 = 0000010100
// OR
fmt.Printf("Bitwise OR: %d - %.10b\n", a | b, a | b)
// 0011010101 OR 0000010100 = 0011010101
// XOR
fmt.Printf("Bitwise XOR: %d - %.10b\n", a ^ b, a ^ b)
// 0011010101 OR 0000010100 = 0011000001
fmt.Printf("Bitwise NOT: %d - %.10b\n", ^a, ^a)
// NOT 0011010101 = 1111111100101010Output:
Bitwise AND: 20 - 0000010100
Bitwise OR: 213 - 0011010101
Bitwise XOR: 193 - 0011000001
Bitwise NOT: 65322 - 1111111100101010In the case of NOT, a larger binary number is seen compared to the previous ones. This is because for the previous cases, we had leading zeros that didn't represent anything, but when performing a NOT operation, those zeros are converted to ones that now represent values.
It will fill with ones up to the capacity of the variable, in this case, 16 bits.
To use the NAND, NOR, and XNOR operators, we do the same as in the previous example but add a NOT to each one.
For example, if we want to perform a NAND operation, we take the NOT of an AND operation.
// NAND
fmt.Printf("Bitwise NAND: %d - %.10b\n", ^(a & b), ^(a & b))
// NOT (0011010101 AND 0000010100) = 1111111111101011
// 0011010101 NAND 0000010100 = 1111111111101011
// NOR
fmt.Printf("Bitwise NOR: %d - %.10b\n", ^(a | b), ^(a | b))
// NOT (0011010101 OR 0000010100) = 1111111100101010
// 0011010101 NOR 0000010100 = 1111111100101010
// XNOR
fmt.Printf("Bitwise XNOR: %d - %.10b\n", ^(a ^ b), ^(a ^ b))
// NOT (0011010101 XOR 0000010100) = 1111111100111110
// 0011010101 XNOR 0000010100 = 1111111100111110Output:
Bitwise NAND: 65515 - 1111111111101011
Bitwise NOR: 65322 - 1111111100101010
Bitwise XNOR: 65342 - 1111111100111110Example
We are going to perform a small example using roles. We will have the roles READ, WRITE, UPDATE, and DELETE, each of which will be represented by binary numbers with only a 1 in different positions:
| Role | Value |
|---|---|
| READ | 0001 |
| WRITE | 0010 |
| UPDATE | 0100 |
| DELETE | 1000 |
We are going to do it this way so that we can add them up and based on a number (the sum of the roles we want to assign to a profile), we can identify which roles the profile has assigned.
So let's define those 4 variables that will represent the roles:
READ_ROLE := 1 // 0001
WRITE_ROLE := 1 << 1 // 0010
UPDATE_ROLE := 1 << 2 // 0100
DELETE_ROLE := 1 << 3 // 1000Then we are going to assign roles to a profile. We will add the roles for writing, reading, and deleting:
myProfile := READ_ROLE + WRITE_ROLE + DELETE_ROLE
// Profile: 1011And now, to validate if the profile has permissions to perform an operation, we will use the bitwise AND operator:
- If the result of the AND operation is equal to the ROLE, then it has permissions.
- If the result of the AND operation is zero, then it does NOT have permissions.
| Role | Role Value | Profile | AND Result |
|---|---|---|---|
| READ | 0001 | 1011 | 0001 |
| WRITE | 0010 | 1011 | 0010 |
| UPDATE | 0100 | 1011 | 0 |
| DELETE | 1000 | 1011 | 1000 |
// Validating for the update role, it does not have permissions.
fmt.Println("Does the user have permissions to perform the operation?")
if (0 != (myProfile & UPDATE_ROLE)) {
fmt.Println("Yes! :D")
}else{
fmt.Println("No :(")
}// Validating for the read role, it has permissions.
fmt.Println("Does the user have permissions to perform the operation?")
if (0 != (myProfile & READ_ROLE)) {
fmt.Println("Yes! :D")
}else{
fmt.Println("No :(")
}Conclusion
In this article, we have explored the fundamentals of binary operators in Golang and learned how to effectively use them in our applications. We have seen how these operators allow us to perform logical and arithmetic operations at the bit level, which is useful in specific scenarios. Remember that understanding and correctly applying binary operators can improve the performance and efficiency of your programs. Feel free to experiment with them and further explore the power of binary operators in your Go projects!

